Comprends un lot de 2 livrets : leçons et matériels. Ils peuvent être utilisés par les enfants, les parents ainsi que les professeurs. Ce livret comprend la formation 12-18 ans en Montessori et plus qui correspond au programme du collège au lycée en termes d'éducation nationale, ils sont conformes aux savoirs disciplinaires.

Mon livret de géométrie 2 peut être commencé par un enfant d'environ 12 ans voir 10 ans selon les enfants.

Ce livret est extrêmement bien détaillé par des illustrations à chacune des étapes. Le langage est adapté aux enfants pour une meilleure compréhension. La progression du livret est complète et ne requiert aucun matériel Montessori à côté, il suffit juste de le suivre dans l'ordre. Ces livrets sont aussi adaptés aux enfants avec des troubles, dys, tdah, autiste, qui ont des problèmes de concentration car ils sont épurés, ils ne retiennent que l'essentiel sans superflu.


Le sommaire est détaillé comme suit:

Égalité, similitude et équivalence
Concept d'égalité
Concept de similitude (semblable)
Concept d’équivalence
Activités pour renforcer la notion d’équivalence

Les équivalences des triangles constructeurs
La boîte triangulaire
La petite boîte hexagonale
La grande boîte hexagonale
La petite boîte hexagonale et la boîte triangulaire
La boîte rectangulaire des triangles bleus
La boîte des triangles constructeurs bleus

Quels matériaux sont nécessaires à la géométrie ?
Le compas
Le rapporteur
L'équerre

Les polygones
Concept de polygone
Les polygones réguliers
Les parties d'un polygone régulier
Comment tracer la médiatrice d’un segment ?
Comment trouver le centre d’un polygone régulier ?
Comment trouver un des rayons de mon polygone ?
Comment trouver un des apothèmes de mon polygone régulier ?
Que veut dire « polygone » ?
Les parties du triangle équilatéral et du triangle isocèle
Les parties du triangle rectangle
Les parties du carré et du losange
Les parties du trapèze
Les types de quadrilatères
L’arbre généalogique des quadrilatères
Les diagonales des polygones
Le nombre de diagonales dans les polygones
 
Les angles
Les types de triangles selon les angles
Le rapporteur
L'histoire du rapporteur
Mesurer avec le rapporteur
Additionner les angles
Soustraire les angles
Multiplier les angles
Diviser les angles
Tracer des angles
La bissectrice
Le nom des angles et leurs degrés
Les sommes des angles des polygones

Le centre de gravité d'une figure
Qu’est-ce que le centre de gravité d’une figure ?

Les figures inscrites et circonscrites
Le triangle équilatéral inscrit dans un autre triangle équilatéral
Comment inscrire un triangle dans un cercle ?
Le triangle équilatéral inscrit dans l’hexagone
Le cercle inscrit dans un triangle équilatéral

Les cercles
Le vocabulaire
Les relations entre les cercles et les lignes
Les relations entre deux cercles
La circonférence et PI

Les équivalences
L'équivalence sensorielle du triangle
L'équivalence sensorielle du losange
L'équivalence sensorielle du trapèze
L'équivalence sensorielle du décagone 1
L'équivalence sensorielle du décagone 2
Le raisonnement de l'équivalence du triangle
Le raisonnement de l'équivalence du losange
Le raisonnement de l'équivalence du trapèze
Le raisonnement de l'équivalence du décagone 1
Le raisonnement de l'équivalence du décagone 2
Histoire de Pythagore
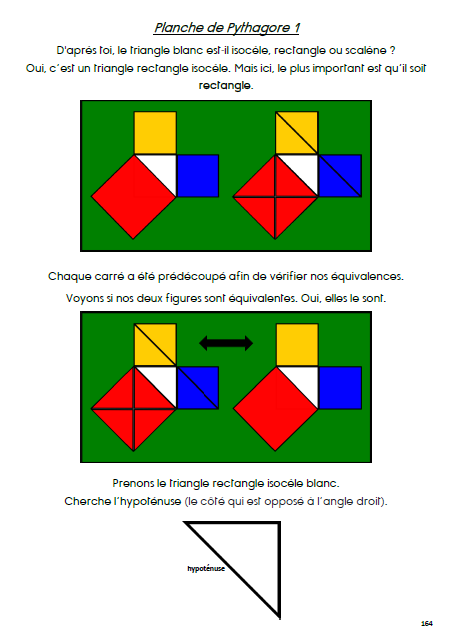
Planche de Pythagore 1
Planche de Pythagore 2
Pythagore avec les triangles constructeurs
Exploration du théorème de Pythagore avec la planche d'Euclide
La planche d'Euclide
Application du théorème de Pythagore

La trigonométrie
Sais-tu ce qu’est la trigonométrie ?
Quelle formule dois-je utiliser ?
Qu’est-ce qu’une formule inverse ?
Application du théorème de Pythagore

L'aire des figures planes
Présentation du matériel
L'aire des rectangles
L’aire des parallélogrammes
L’aire d’un triangle isocèle
L’aire des triangles rectangles
L’aire des triangles obtusangles
Récapitulatif des formules
Le triangle
Le parallélogramme : méthode 1
Le parallélogramme : méthode 2
Le parallélogramme : méthode 3
Le parallélogramme : méthode 4
Le trapèze
Le décagone : méthode 1
Le décagone : méthode 2
Le décagone : méthode 3
Le pentagone
L’aire d’un cercle

Les solides
Révision du vocabulaire et nouvelles notions
Construction d’un solide
Equivalence des solides
Le rhomboïde
Le prisme triangulaire
Le prisme hexagonal
Le polyèdre
La surface du prisme rectangulaire
La surface du prisme triangulaire
La surface du cylindre
La surface de la pyramide à base carrée
La surface du cône

Les volumes
La notion de volume
Comparaison de solides construits avec des cubes
Les 3 dimensions et le volume d'un prisme rectangulaire
Volume d'un prisme rhombique
Volume d'un prisme triangulaire
Volume d'un prisme hexagonal
Le volume contenu dans une pyramide à base carrée
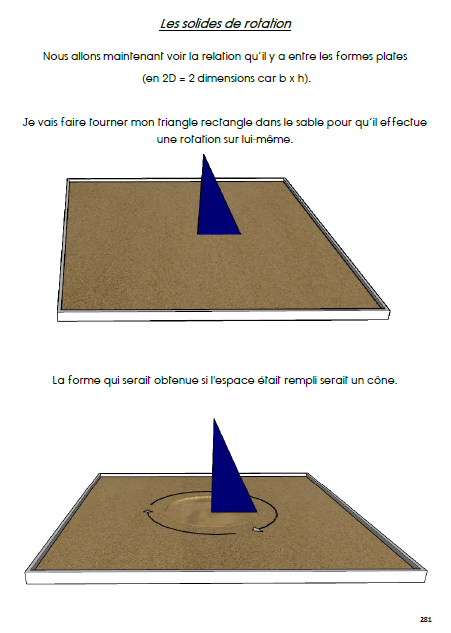
Les solides de rotation
Volume du cylindre
Volume du cône
Volume de la sphère

Proportionnalité et segment
Le rapport entre deux segments
Histoire de Thalès
À quoi sert le théorème de Thalès
Quand est-ce que je peux utiliser Thalès sur une figure ?
Que nous dit le théorème de Thalès ?